متعلق به: مکانیک آسمانی
همچنین نگاه کنید به: قوانین کپلر ، سیاه چاله
چهار نیروی اساسی
در فیزیک ما چهار نیروی اساسی می شناسیم (چهار فعل و انفعالات اساسی) – همچنین نگاه کنید به: مدل استاندارد فیزیک ذرات بنیادی [19659004] جاذبه
گرانش با سه نیرو دیگر (فعل و انفعالات) متفاوت است زیرا:
- گرانش بسیار ضعیف تر از بقیه است
- جاذبه را نمی توان محافظت کرد (اگر اصطلاحاً سیستم های اینرسی وجود نداشته باشد)
- جاذبه است همیشه جذاب ، هرگز دافعه
قانون جاذبه
در سال 1668 ، آیزاک نیوتون (1642-1727) قانون معروف جاذبه را تدوین کرد:
( بزرگ F = G frac {m cdot M} {r ^ 2} )
که می توان قوانین کپلر را از آن استخراج کرد …
آنچه در دانش نیوتن ویژه است ، نه تنها فرمول بندی به عنوان یک فرمول واحد است ، بلکه همچنین این است که نیروی گرانش بین همه اجسام جهان عمل می کند. به عنوان مثال ، قمرهای مشتری طبق این قانون به دور مشتری می چرخند و ستاره های دوتایی و غیره نیز به دلیل جاذبه به دور یکدیگر می چرخند …
آیزاک نیوتن نیز تحقیقات زیادی در مورد نور انجام داد. کلمات کلیدی برای این امر عبارتند از: بازتاب جزئی ، حلقه های نیوتن ، …
اندازه ثابت گرانش G فقط خیلی بعد توسط آزمایش معروف "تعادل جاذبه" توسط هنری کاوندیش (1731-1810) تعیین شد .
در ویکی پدیا می یابیم:
( Large G = (6 {،} 674 ، 30 pm 0 {،} 000 ، 15) cdot 10 ^ {- 11} ، mathrm { frac {m ^ {3}} {kg cdot s ^ {2}}} )
جاذبه
همانطور که همه ما از مدرسه می دانیم ، دارای شتاب گرانشی تقریباً 9.81 متر بر ثانیه بر روی سطح زمین هستیم 2
ما همچنین می توانیم از قانون جاذبه استفاده کنیم (نگاه کنید به بالا) بنویسید به عنوان:
( Large a = G frac {M} {r ^ 2} )
اگر از نیرو = جرم برابر شتاب ، یعنی F = m * a استفاده کنیم.
اگر میانگین شعاع زمین را 6371 کیلومتر فرض کنیم ، در فاصله زمین 6371 کیلومتر از مرکز زمین قرار داریم.
طبق ویکی پدیا ، جرم زمین تقریباً 5/9772 * 10 24 کیلوگرم
است. با شعاع زمین شناخته شده ، جرم زمین شناخته شده و ثابت گرانش ، می توان میانگین شتاب گرانشی سطح زمین را محاسبه کرد:
( Large a = G frac {5.9772 cdot 10 ^ {24}} {6371000 ^ 2} = 9.82 )
یا برعکس: اگر کسی شتاب گرانشی را اندازه گیری کرده باشد ، شعاع زمین را بداند و ثابت گرانش را اندازه گیری کند (مانند هنری کاوندیش) ، می توان جرم زمین را تعیین کرد …
مسیر دایره ای
برای یک مسیر دایره ای با شعاع R یکی خواهد بود نیروی مرکز گرا مورد نیاز:
(F_Z = m cdot frac {v ^ 2} {R} )
چنین نیرویی از نوع گریز از مرکز ناشی از جاذبه بدن مرکزی جرم M است. این نیروی گرانش:
(F_G = G cdot frac {m cdot M} {R ^ 2} )
از نظر ریاضی ، این منجر به سرعت مداری می شود (اصطلاحاً اولین سرعت کیهانی):
(v_1 = sqrt { frac {G cdot M} {R}} )
معنی زمین: 91/7 کیلومتر بر ثانیه.
این یک مسیر دایره ای (نظری) با شعاع R خواهد بود. بنابراین ارتفاع صفر متر از سطح زمین است. بیایید یک مثال واقع بینانه بگیریم: ISS. این پرواز در ارتفاع حدود 400 کیلومتری پرواز می کند. این ما را به سرعت
برساند
( Large v = sqrt { frac {6.6743 cdot 10 ^ {- 11} cdot 5.9772 cdot 10 ^ {24}} {6371000 + 400000}} = 7.94 enspace km / s )
سرعت فرار
برای اینکه جسمی به وزن متر از سطح زمین فرار کند ، به انرژی جنبشی نیاز دارد که حداقل به اندازه انرژی بالقوه آن باشد:
(E_ {kin} = frac {m} {2} cdot v ^ 2 )
پتانسیل جاذبه روی سطح زمین:
(E_ {pot} = int limit _ {- infty} ^ {R} G cdot frac {m cdot M} {r ^ 2} dr = G cdot m cdot M cdot سمت چپ [ -frac{1}{r} right] _ {- infty} ^ R = -G cdot m cdot M cdot frac {1} {R} )
از نظر ریاضی ، سرعت فرار (اصطلاحاً سرعت دوم کیهانی) نتیجه:
(v_2 = sqrt { frac {2 cdot G cdot M} {R}} )
مفهوم زمین: 11.2 کیلومتر بر ثانیه
این عدد منحصراً بر اساس گرانش زمین است. باید به معنای تأثیرات دیگری مانند چرخش زمین یا هر نوع مانور چرخشی باشد که می تواند این سرعت مورد نیاز را کاهش دهد – مانند پروازهای ماه یا کاوشگرهای فضایی ویجر …
همچنین نگاه کنید به: https://de.wikipedia.org/wiki/Fluchtfrequenz_(Raumfahrt)
سیاهچاله
در مورد سیاهچاله ، سرعت فرار سرعت نور c خواهد بود. اگر v 2 = c قرار دهیم به دست می آوریم:
(c = sqrt { frac {2 cdot G cdot M} {R}} )
حل شعاع R منجر به:
(R = frac {2 cdot G cdot M} {c ^ 2} )
با چنین شعاعی هیچ نوری نمی تواند فرار کند. بنابراین این اشیا “" سیاهچاله ها "نامیده می شوند. با شعاع کوچکتر ، سرعت فرار از سرعت نور بیشتر خواهد بود. با شعاع بزرگتر سرعت فرار کمتر از سرعت نور خواهد بود. به این شعاع " شعاع شوارتزیلد " یا افق رویداد گفته می شود. . جالب توجه است که فرمول افق رویداد (شعاع شوارتزیلد) برای GTR همان چیزی است که در اینجا در "محاسبه شیر مادر" آمده است.
نظریه عمومی نسبیت (GTR)
GTR براساس فرض معادل گرانش و شتاب است
این اصل برابری منجر به انحراف نور در میدان های گرانشی می شود.
اگر کسی همچنان بخواهد فرض کند که نور همیشه کوتاه ترین مسیر را طی می کند ، گرانش باید فضا را بر این اساس منحنی کند .
. انحنا
انحنای یک شی هندسی به عنوان انحراف از یک مسیر مستقیم شناخته می شود. این نیاز به (حداقل) یک بعد اضافی دارد که در آن انحنا اجرا شود.
مرحله 1: انحنای یک خط در صفحه
ما یک خط مستقیم را در نظر می گیریم. تا زمانی که واقعاً مستقیم باشد خمیده نیست. اگر یک انحنا به سمت چپ (یا راست) ایجاد کند ، ما یک انحنا داریم – و برای این امر حداقل (بعد) به بعد دوم نیاز داریم.
قدرت انحنا می تواند کم و بیش ملایم یا قوی تر باشد. ما قدرت انحنا را در یک نقطه با استفاده از به اصطلاح دایره انحنا اندازه می گیریم. این یک دایره است که به بهترین وجهی با منحنی در نقطه مورد بررسی متناسب است. انحنای بزرگ به معنای انحنای کوچک و انحنای کوچک به معنای انحنای قوی است. متغیر شعاع اندازه گیری قدرت انحنا است.
برای تابعی y = f (x) که می توان دو بار از هم تفکیک کرد ، شعاع انحنا در یک نقطه x است:
( Large r (x) = left vert frac {(1+ (f ^ prime (x)) ^ 2) ^ frac {3} {2}} {f ^ { prime prime} (x)} راست vert
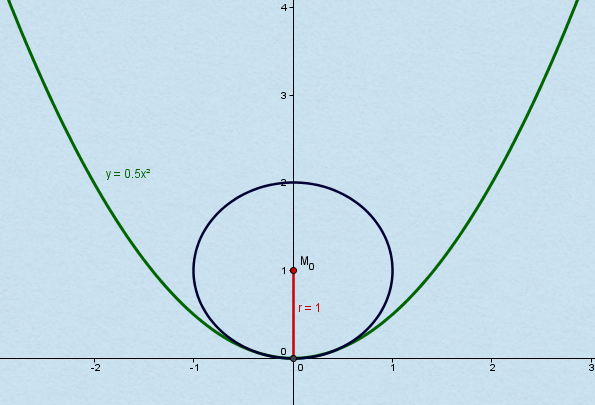
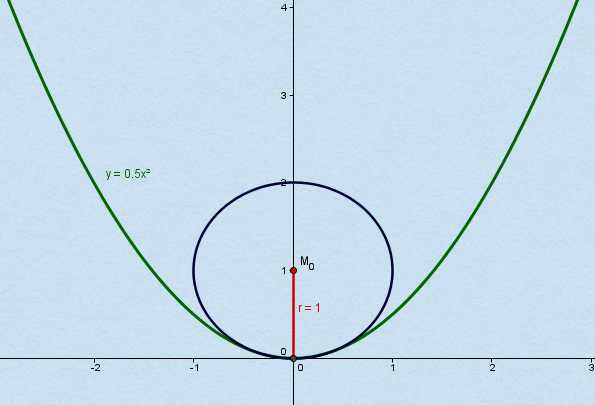
به عنوان مثال ما یک parabola f (x) = 0.5 * x 2
در نظر می گیریم. برای این منظور مشتقات داریم:
f " (x) = x
f " (x) = 1
شعاع انحنا به عنوان مثال در نقطه x 0 = 0 سپس مطابق فرمول فوق است:
( Large r (x_0) = frac {(1+ {x_0} ^ 2) ^ { frac {3} {2}}} {1} = 1 )
من این مثال را از https://www.ingenieurkurse.de/hoehere-mathematik-analysis-gewoehnliche-d متفاوت :
مرحله 2: انحنای یک سطح در فضا
به طور مشابه ، می توان سطوح منحنی را در فضا تصور کرد. اما در اینجا شعاع انحنا می تواند در جهات مختلف متفاوت باشد. در حدود روشی که ما آن را از یک شیب می شناسیم.
مرحله 3: انحنای فضا
xyz
مرحله 4: انحنای فضا-زمان
xyz
.