متعلق به: فیزیک
همچنین نگاه کنید به: نظریه نسبیت ، فضای بردار ، جاذبه ، سیاهچاله ها
انحنای زمان-زمان
نظریه عمومی نسبیت (ART) بر اساس فرض برابری گرانش و شتاب است.
انحراف نور در میدانهای گرانشی ناشی از این اصل برابری است.
اگر کسی بخواهد فرض کند که نور همیشه کوتاهترین مسیر را طی می کند ، جاذبه باید فضا (زمان بهتر) را خم کند بنابراین متریک بوجود می آید که در آن کوتاهترین مسیر بین دو نقطه لزوماً خط مستقیم اقلیدسی نیست.
اول از همه ، ما می خواهیم در مورد اصطلاح "انحنا" به طور کلی بحث کنیم.
انحنا در معیارهای اقلیدسی [19659003انحناییکشیهندسیبهمعنایانحرافازمسیرمستقیم است. این امر به (حداقل) یک بعد دیگر نیاز دارد که در آن انحنا اجرا شود یا اصطلاح "مستقیم" باید دوباره تعریف شود (نگاه کنید به: غیر اقلیدسی).
ما یک خط مستقیم را در نظر می گیریم. تا زمانی که واقعاً مستقیم باشد ، خمیده نیست. اگر یک منحنی به سمت چپ (یا راست) ایجاد کند ، یک منحنی داریم – و برای این منظور (حداقل) به بعد دوم نیاز داریم. قدرت منحنی می تواند کم و بیش ملایم یا قدرتمندتر باشد. ما قدرت انحنا را در یک نقطه با استفاده از به اصطلاح دایره انحنا اندازه می گیریم. این یک دایره است که به بهترین وجهی با منحنی در نقطه مورد بررسی متناسب است. انحنای بزرگ به معنای انحنای کوچک و انحنای کوچک به معنای انحنای قوی است. متقابل شعاع اندازه گیری قدرت انحنا است.
س otherال دیگر این است که کدام اشیا ge هندسی وجود دارد که "خمیده" می شوند؟ در ساده ترین حالت این یک خط یک بعدی در یک صفحه دو بعدی است. بنابراین به عنوان مثال نمودار تابع یا به اصطلاح منحنی. منحنی ها در این زمینه به عنوان زیرمجموعه ای از یک فضای بردار بسیار جالب توجه هستند که می توانند با نگاشت یک بازه واقعی در فضای بردار ، به عنوان منحنی به اصطلاح "پارامتر شده" نشان داده شوند. "پارامتر سازی مجدد" سپس یک رابطه هم ارز بین منحنی های پارامتر شده است. سپس یک "منحنی" را می توان به عنوان کلاس معادل سازی چنین منحنی های پارامتر شده درک کرد. به عنوان نماینده یک کلاس هم ارز ، دوست دارد یک منحنی را با توجه به طول قوس پارامتر کند.
اگر با منحنی و سپس به ویژه با طول یک منحنی یا انحنای منحنی ، ما با هندسه دیفرانسیل سر و کار داریم.
تعدادی فیلم YouTube بسیار خوب برای این وجود دارد:
مرحله 1: انحنای یک خط در صفحه
اگر اگر جسم مورد بررسی یک نمودار تابعی باشد ، به عنوان مثال y = f (x) در صفحه ، به راحتی می توانیم انحنا را محاسبه کنیم:
برای یک تابع دو برابر قابل تغییر y = f (x) شعاع انحنای در یک نقطه x:
( Large r (x) = left vert frac {(1+ (f ^ prime (x)) ^ 2) ^ frac {3} {2}} {f ^ { prime prime} (x)} راست vert )
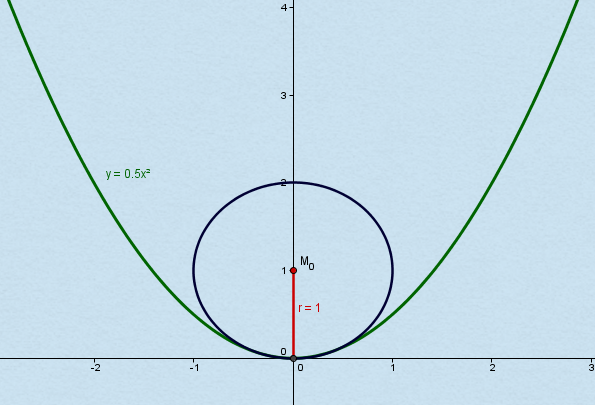
به عنوان مثال ما یک parabola f (x) = 0.5 * x 2
در نظر می گیریم. برای این منظور مشتقات داریم:
f " (x) = x
f " (x) = 1
شعاع انحنا به عنوان مثال در نقطه x 0 = 0 مطابق فرمول فوق است:
( Large r (x_0) = frac {(1+ {x_0} ^ 2) ^ { frac {3} {2}}} {1} = 1 \ )
و به عنوان آزمون 1 = x می گیریم:
( Large r (1) = frac {(1 + 1 ^ 2) ^ { frac {3} {2}}} {1} = 2 ^ frac {3} {2} = 2 sqrt { 2} )
من این مثال را از https://www.ingenieurkurse.de/hoehere-mathematik-analysis-gewoehnliche-diversity :
مرحله 2: انحنای یک منحنی در صفحه
اگر جسم مورد بررسی یک منحنی "صحیح" در صفحه باشد ، انحنا به گونه دیگری محاسبه می شود.
به عنوان یک منحنی "صحیح" (در صفحه) ) قطعه منحنی را از x = -1 تا x = 1 از پارابلای فوق در نظر می گیریم. به عنوان یک منحنی پارامتر شده ، جایی که پارامتر t نیز ممکن است از -1 به 1 اجرا شود (که مثلاً می توانیم آن را به عنوان زمان تصور کنیم) به این شکل است:
( Large alpha (t) = left ( start {array} {c} t \ frac {1} {2} t ^ 2 end {array} right) \ )
برای محاسبه انحنا ، ابتدا تعیین می کنیم:
( Large alpha ^ prime (t) = left ( start {array} {c} 1 \ t end {array} right) )
که پس از آن:
( Large || alpha ^ prime (t) || ^ 2 = 1 + t ^ 2 \ )
و با:
( Large alpha ^ { prime prime} (t) = left ( start {array} {c} 0 \ 1 end {array} right) )
نتایج در:
( Large det ( alpha ^ prime (t) ، alpha ^ { prime prime} (t)) = 1 \ )
و نتیجه آن انحنا است:
( Large kappa_ alpha (t) = frac {1} {(1 + t ^ 2) ^ frac {3} {2}} )
در t = 0 انحنای زیر است:
( Large kappa_ alpha (0) = 1 \ )
و به عنوان آزمون 1 = t می گیریم:
( Large kappa_ alpha (1) = frac {1} {2 sqrt {2}} \ )
از آنجا که t = x ، این دقیقاً مربوط به محاسبات شعاع انحنا است (به مرحله 1 بالا نگاه کنید).
مرحله 3: انحنای یک سطح در فضا
به طور مشابه ، می توانیم سطوح خمیده را در فضا تصور کنیم. اما در اینجا شعاع انحنا می تواند در جهات مختلف متفاوت باشد. تقریباً به همان روشی که ما آن را از یک شیب می شناسیم.
در این مورد نیز ما آن را به شکل هندسی کاملاً کلاسیک به صورت خمیدگی به بعد دیگر تصور می کنیم.
انحنا با استفاده از معیارهای غیر اقلیدسی
در نسبیت عام ، صحبت می شود همچنین از "انحنا" به عنوان مثال انحنای فضا یا انحنا of زمان-زمان. "متریک" قانونی است که فاصله را به دو نقطه در فضای مربوطه اختصاص می دهد. چنین معیاری سپس بطور خودکار طول خطوط را تعریف می کند …
خط ژئودتیک
خطی که کوتاهترین ارتباط بین دو نقطه را تشکیل می دهد ، ژئودزیک یا همچنین خط ژئودزیک نامیده می شود ] در سطح زمین می دانیم که به عنوان مثال در دریانوردی یا هواپیمایی اگر مسیر پرواز از لندن به لس آنجلس را در نظر بگیریم ، به عنوان مثال:
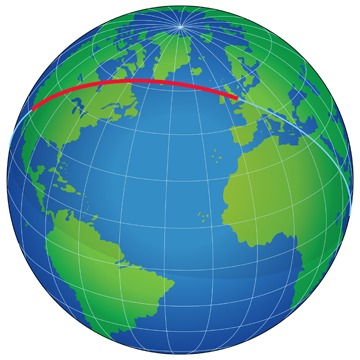
نور همیشه بر روی ژئودزیك كار می كند ، بنابراین كوتاه ترین اتصال را طی می كند. این می تواند "منحنی" به نظر برسد …
انحنای بدون بعد اضافی
برای چنین انحنایی لزوماً به بعد بعدی احتیاج نداریم. همچنین انحنا می تواند توسط خود قوانین دیگر مسافت (= معیارها) ایجاد شود.
به متریک شوارتزشیلد مراجعه کنید
تعدادی فیلم YouTube بسیار خوب برای این وجود دارد:
در نظر می گیریم. برای این منظور مشتقات داریم:
f " (x) = x
f " (x) = 1
شعاع انحنا به عنوان مثال در نقطه x 0 = 0 مطابق فرمول فوق است:

( Large alpha (t) = left ( start {array} {c} t \ frac {1} {2} t ^ 2 end {array} right) \ )

به متریک شوارتزشیلد مراجعه کنید
.
